Wall thickness
It is essential to determine the wall thickness of plastic parts reasonably. Other shapes and sizes, such as reinforcement bars and rounded corners, are based on the wall thickness as a reference. The wall thickness of plastic products is mainly determined by the use of plastic requirements; that is, the product needs to withstand external forces, whether as a support for other parts, the choice of plastic material properties, weight, electrical properties, dimensional accuracy, and stability and assembly and other requirements.
The general thermoplastic wall thickness ranges from 1 to 6 mm. The most commonly used is 2 to 3 mm. large parts are also available over 6 mm. Table 1 shows the recommended wall thickness of some thermoplastics.
Plastic Material | Minimum | Small Parts | Medium-sized Parts | Large Parts |
| Nylon | 0.45 | 0.76 | 1.5 | 2.4~3.2 |
| Polyethylene | 0.6 | 1.25 | 1.6 | 2.4~3.2 |
| Polystyrene | 0.75 | 1.25 | 1.6 | 3.2~5.4 |
PMMA | 0.8 | 1.5 | 2.2 | 4~6.5 |
PVC | 1.2 | 1.6 | 1.8 | 3.2~5.8 |
PP | 0.85 | 1.54 | 1.75 | 2.4~3.2 |
PC | 0.95 | 1.8 | 2.3 | 3~4.5 |
POM | 0.8 | 1.4 | 1.6 | 3.2~5.4 |
ABS | 0.8 | 1 | 2.3 | 3.2~6 |
Common wall thickness design defects:
- wall thickness is not uniform
Uniform wall thickness is a major principle of the design of plastic parts. If the wall thickness is not uniform, it will make the plastic melt filling speed, and cooling shrinkage is not uniform, which will cause depression, vacuum bubbles, warpage, and even cracking, or even lead to shrinkage marks, thermal stress, deflection part distortion, different colors or different transparency. When taking smaller wall thicknesses, the strength and stiffness of the product will be poor in use and assembly. From an economic point of view, too thick products not only increase the material cost but also prolong the production cycle. The thick glue area cools slower than the next thin glue area, thus creating shrinkage marks. Figure 1 below shows the design of uniform wall thickness.
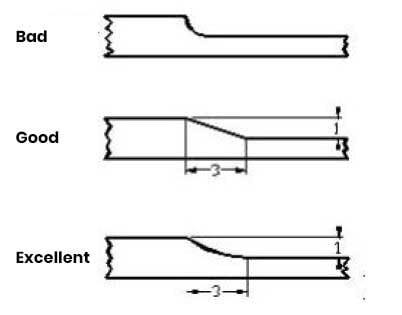
If it is inevitable that the thicker areas become thinner, try to design a gradual change in the wall thickness within a ratio of 3:1, as shown in Figure 2 below.
In fact, most of the thicker glues can be designed with ribbing to change the total wall thickness. Besides saving material and production costs, it can also save cooling time, approximately proportional to the wall thickness.
In addition, the wall thickness design also considers the Mold Flow, i.e., the distance of the melt from the injection molding gate to each part of the cavity. If the ratio of mold flow to wall thickness is too large, the place far from the gate will be short of material, which is often said to be not full. Therefore, if necessary, the wall thickness should be increased.
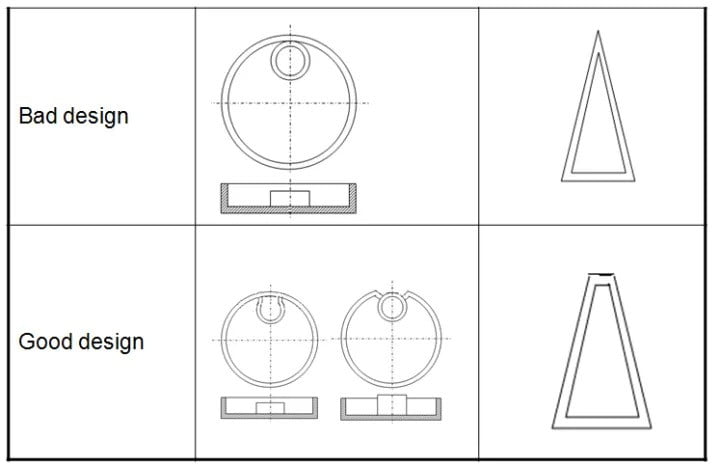
- Sharp corners
Sharp corners usually lead to defective parts and stress concentrations. The location of sharp corners often causes undesired material accumulation after post-treatment processes, such as plating and painting. Concentrated stress areas can break under load or impact, so we should design to avoid sharp corners. Figure 3 below can be used for reference.
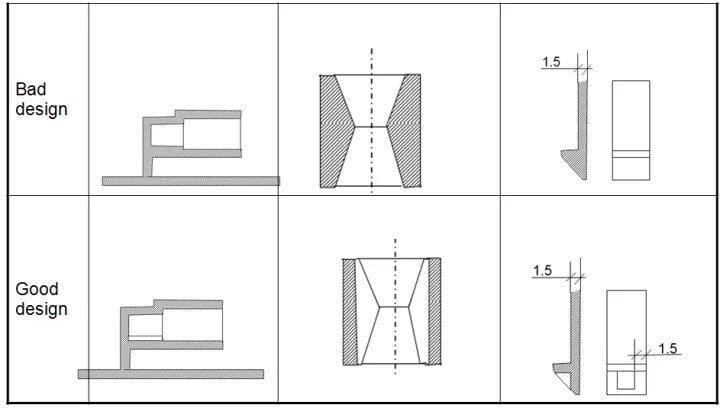
Mold Unmolding Direction And Draft Taper
Each injection molded product should first determine its mold parting direction and parting line at the beginning of design to ensure that the damage to the core extraction mechanism is minimized and the impact of the parting line on the appearance is eliminated. After the mold parting direction is determined, the product’s structure, such as ribs, snaps, and bumps, should be designed to be consistent with the mold parting direction as much as possible to avoid core extraction, reduce the parting line and prolong the mold life. After the mold opening direction is determined, appropriate parting lines can be selected to improve the appearance and performance.
Releasing the injection molded part from the molding mold involves overcoming the unmolding and mold opening force. The molded part shrinks during the cooling process, and the hole wall part exerts a clamping force on the core. Friction between the molded part and the core during mold opening, vacuum adsorption on the bottom seal of the hole during mold opening, and many other factors cause the demolding force to be much larger than the mold opening force. Excessive demolding force can cause deformation, whitening, wrinkling, and surface abrasion. The draft taper is a significant factor of the demolding force. To make the product wall thickness uniform and prevent the product from attaching to the hotter concave mold after the mold is opened, the release angle should be equal for both the concave and convex mold. However, in exceptional cases, if the product is required to be attached to the concave mold after the mold is opened, the exit angle of the concave mold can be reduced appropriately, or a proper amount of inversion can be deliberately added to the concave mold.
There is no definite size of the draft taper; it is usually determined by experience. Generally speaking, highly polished outer walls can use a 1/8 degree or 1/4 degree exit angle, while deep or woven products require a corresponding increase in the exit angle.
In addition, when considering the draft taper, in principle, the larger of the slope, the better for the release, but one must pay attention to ensure the dimensional accuracy of the plastic parts; the size error caused by the release slope must be controlled within the range of dimensional accuracy. A larger release angle should be considered for the plastic parts with larger shrinkage and complex shapes.
Rib Reinforcement
The strength of a plastic part does not increase precisely according to its wall thickness. On the contrary, the increase in wall thickness causes shrinkage and internal stress but reduces its strength. The strength of plastic parts is based on the stiffness, mainly using a thin-walled style combination structure and set-up reinforcement in the corresponding components to enhance the cross-sectional moment of inertia.
But after adding the rib reinforcement, the connection between the rib and the main wall will become thicker. This thickness usually depends on the full circle of internal tangency, that is, on the rib thickness and the radius of the corner of the root. In Figure 4, the thickness of the base material is 4mm, the thickness of the left example is 4mm, the radius of the root is R2.4, and the maximum diameter of the inner cut circle is φ6.2; in the right example, the thickness of the rib is changed to 2mm, the radius of the root is changed to R1.6, and the maximum diameter of the inner cut circle becomes φ4.9. In Figure 5, due to the increase in the local wall thickness, it is easy to produce shrinkage deformation on the back side, which affects the appearance of the plastic parts. For parts with very high surface requirements, such defects affecting the appearance are unacceptable. The correct design can reduce the possibility of forming surface dents in the component to improve the quality of the part.
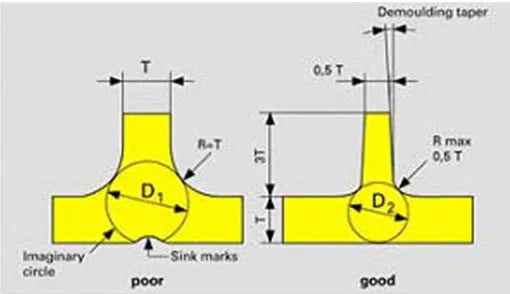
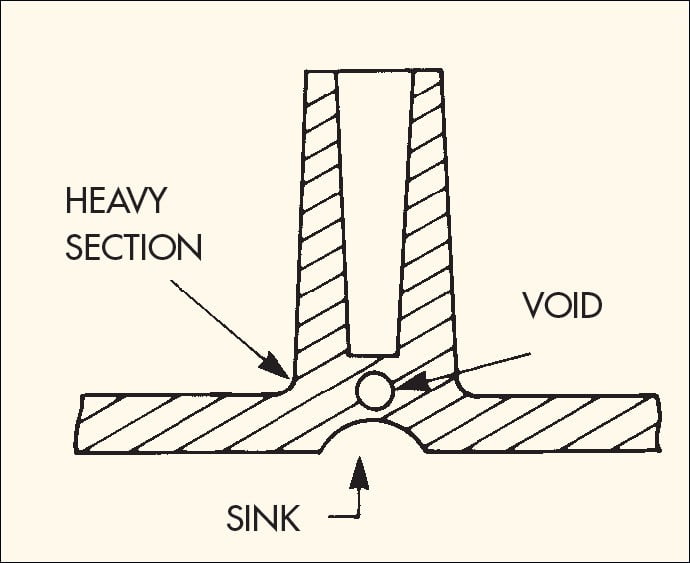
The analysis in Figure 4 shows that the thickness of the tendons should be minimized, but there is a limit to this. If the tendon’s thickness is too small, it is necessary to increase the height of the tendon to increase the stiffness. Tendons are too thin when pressed, tendons easily deformed; the molding material is not easy to fill, sticky on the mold, and other problems. Of course, the radius of the bottom corner of the tendon can not be too small. Otherwise, it will not play a role in reducing stress concentration.
In general, the radius of the rib root fillet should be no less than 40% of the rib thickness, and the rib thickness should be between 50% and 75% of the base material wall thickness, with the higher ratio limited to materials with slight shrinkage. The height of the bar should be less than five times the thickness of the base material. The bars must have draft angles and be placed in the direction of the parting or a movable mold component. The spacing between the bars must be greater than twice the thickness of the base material.
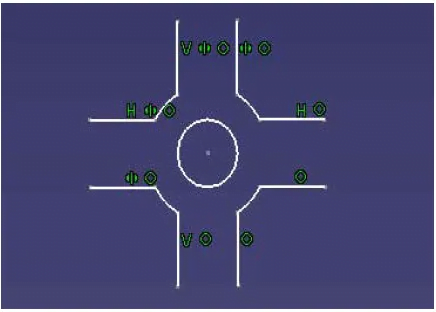
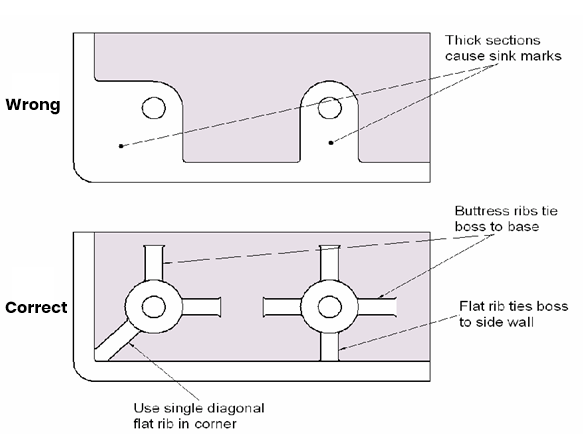
In addition, we usually expect a part to be equally rigid in all directions. The easiest way to obtain this result is to add rib reinforcement to the part in both the transverse and longitudinal directions and make them intersect vertically. However, there is also the problem of increasing the wall thickness at the intersection, increasing the chance of shrinkage. In this case, a circular hole can be added at the intersection to create a uniform wall thickness. Just like the following figure 6: crossbar
Holes
It is common to create holes in plastic parts to join them with other components or to add functional combinations to the product.
The size and location of the holes should be such that they do not affect the strength of the product or increase the complexity of the production, and the following are some of the factors to be considered when designing the holes.
- The distance between the connected holes or the distance between the holes and the straight edges of the adjacent products should not be less than the diameter of the holes, especially the value of the edge should be as large as possible; otherwise, the location of the piercing is prone to fracture. If there is a thread attached to the hole, the distance between the screw hole and the edge of the product is generally greater than three times the diameter of the hole.
- The types of holes are generally through holes, blind holes, and graded holes. From the assembly perspective, the application of through holes is more than blind holes, and it is easier to produce than blind holes. From the mold design point of view, the design of a through-hole will also be more convenient in structure, which can be formed by the combination of two cores fixed on the moving mold and the fixed mold or can be formed by only one core fixed on the moving mold or the fixed mold. The former forms two cantilever beams under the action of fluid plastic, but the force arm is short, and the deformation is not large. The latter has lap joints with both moving and fixed molds and generally forms a simple support beam with slight deformation. When two cores are used, the diameters of the two cores should be slightly different to avoid the product from buckling due to the slight deviation of the axis of the two side pegs, and the two ends of the joint must be ground flat. The core of the blind hole is completely cantilevered, which is easily bent by the impact of fluid plastic, and the formed hole will become a shaped hole. Generally speaking, the depth of the blind hole is limited to twice the diameter. If the diameter of the blind hole is only 1.5mm or less, the depth of the blind hole should not be larger than the size of the diameter. And the wall thickness of the bottom of the blind hole should not be less than one-sixth of the hole diameter; otherwise, there will be shrinkage.
- side holes are often formed by the side core method, which will increase the cost of the mold, and if the side core is too long, it is easy to break, increasing mold maintenance costs. If the conditions permit, the method in Figure 7 below can be used to improve.
Pillars
Pillars with protruding plastic walls assemble products, separate objects, and support other parts. Hollow pillars can be used to insert parts, tighten screws, etc. All of these applications must be strong enough to support pressure without breaking. Pillars are generally made into cylindrical shapes because they are easy to mold and have good mechanical properties.
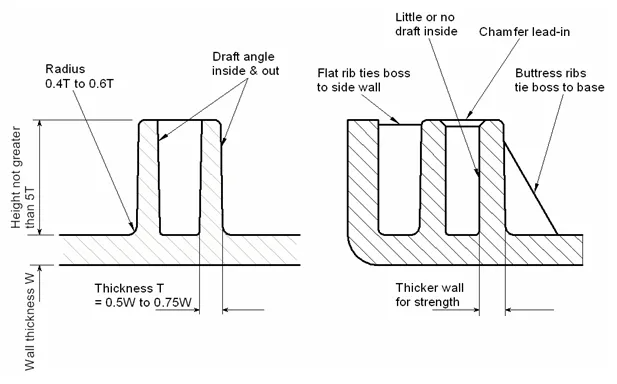
Generally speaking, the pillar should not be designed as an independent cylinder but should be connected to the outer wall or used together with the rib reinforcement as far as possible to strengthen the pillar and make the flow of the melt smoother, the connection with the outer wall should be made into a thin-walled connection to avoid shrinkage, and the bottom of the pillar should be connected to the base material with a corner radius of 0.4 to 0.6 times the thickness of the base material. The wall thickness of the pillar should be between 0.5 and 0.75 of the base material thickness, and the top hole of the pillar should be chamfered to facilitate the installation of the screw guide. The column should have a draft taper. These points are similar to the design requirements of reinforcement bars, so it can also be said that the pillar is a variant of the bar. Please see Figure 8 and Figure 9 below for the corresponding relationships.
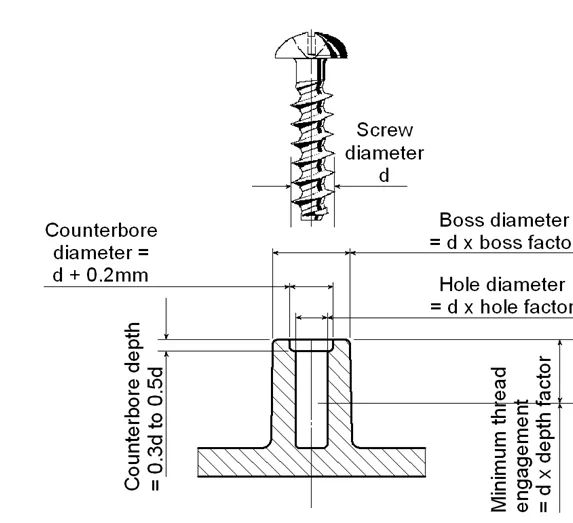
Many pillar tabs are used to attach self-tapping screws. The internal threads on the pillar are formed after assembly by cold flow machining, which does not produce material cutting, but only plastic extrusion deformation to produce the articulated internal threads.
The size of the threaded pillar should be able to withstand both the screw screwing force and the attached load, and the size of the aperture on the pillar should be able to ensure that the screw does not come out under specific torque and specific vibration. The pillar’s outer diameter should ensure the screw is torqued to withstand the resulting circumferential force without breaking or rupturing. In addition, to ensure the convenience of screwing in the self-tapping screw guide, a pit is usually opened at the top of the pillar, and the pit’s diameter should be slightly larger than the nominal diameter of the thread. Calculating the pillar size is very complicated; here, we recommend a simple estimation method; the key to this method is the nominal diameter of the screw. First, you must write the material used, find the corresponding factor from the right side, and multiply the nominal diameter of the screw by the corresponding factor to get the corresponding size. As in Figure 9 and Table 2
Plastic Material | Coefficients of Aperture | Tab Tiameter Coefficients | Thread depth coefficient |
ABS | 0.80 | 2.00 | 2.00 |
ABS/PC | 0.80 | 2.00 | 2.00 |
ASA | 0.78 | 2.00 | 2.00 |
PA 46 | 0.73 | 1.85 | 1.80 |
PA 46 GF30 | 0.78 | 1.85 | 1.80 |
PA6 | 0.75 | 1.85 | 1.70 |
PA 6 GF30 | 0.80 | 2.00 | 1.90 |
PA 66 | 0.75 | 1.85 | 1.70 |
PA 66 GF30 | 0.82 | 2.00 | 1.80 |
PBT | 0.75 | 1.85 | 1.70 |
PBT GF30 | 0.80 | 1.80 | 1.70 |
PC | 0.85 | 2.50 | 2.20 |
PC GF30 | 0.85 | 2.20 | 2.00 |
PE-HD | 0.75 | 1.80 | 1.80 |
PE-LD | 0.75 | 1.80 | 1.80 |
PET | 0.75 | 1.85 | 1.70 |
PET GF30 | 0.80 | 1.80 | 1.70 |
PMMA | 0.85 | 2.00 | 2.00 |
POM | 0.75 | 1.95 | 2.00 |
PP | 0.70 | 2.00 | 2.00 |
Because the performance of plastic is not very stable compared to metal materials, so according to the above calculation of the pillar size, it does not necessarily fully meet the requirements; the specific situation will be determined according to the relevant material parameters provided by the material supplier, important occasions must do experiments to verify.
Snap
Snap assembly is a convenient, cost-effective, and eco-friendly connection method because the combined part of the snap is formed simultaneously when the finished product is produced. No other locking accessories, such as screws, are required for assembly.
The principle of the snap is to push the projection on one part through the obstacle on another part in the process of pushing the elastic deformation when through the obstacle to restore the original state of the two together, such as in Figure 10. snap connections, there are permanent and detachable two kinds.

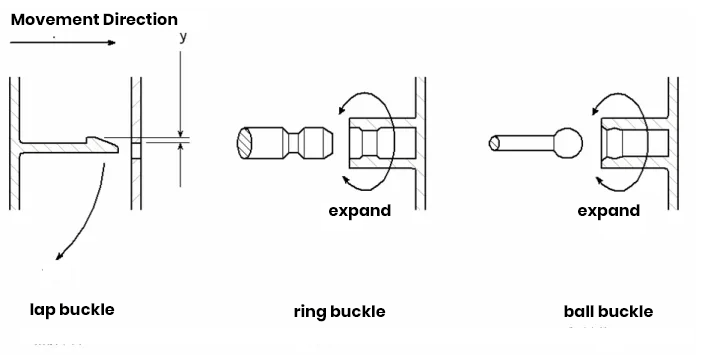
The structural form can be divided into lap buckle, ring buckle, and ball buckle three types, as shown in Figure 11
There are generally two critical angles on the butt snap hook: the disengagement angle and the bite angle; generally, the disengagement angle is larger to achieve a harder disengagement if when the disengagement angle is close to 90 degrees, it becomes a permanent snap. The specific relationship is shown in Figure 12.
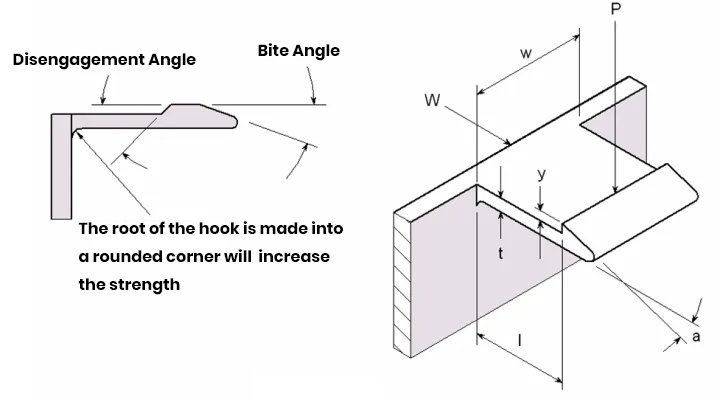
The following formula can calculate the maximum allowable deflection of the equal-section snap:
- Y=el2/(1.5t)
This formula is used when only the snap hook is deformed; in practice, there is also a small amount of deformation near the part where the snap is located, which can be used as a safety factor.
The force required to push the snap to produce Y deformation is calculated using the following formula:
- P = wt2Ee/(6l)
The following formula estimates the required assembly force:
- W=P(μ+tga)/(1-tga)
The detachable snap-off force can also be calculated using the above formula; simply replace a with b.
Table 3 shows some of the coefficients needed for the calculation process.
Plastic Material | Allowed Strain Variables (e)(%) | Bending Modulus (GPa) | Friction Coefficient |
PS | 2 | 3.0 | 0.3 |
ABS | 2 | 2.1 | 0.2 |
SAN | 2 | 3.6 | 0.3 |
PMMA | 2 | 2.9 | 0.4 |
LDRE | 5 | 0.2 | 0.3 |
HDPE | 4 | 1.2 | 0.3 |
PP | 4 | 1.3 | 0.3 |
PA | 3 | 1.2 | 0.1 |
POM | 4 | 2.6 | 0.4 |
PC | 2 | 2.8 | 0.4 |
The ring snap is used to achieve the purpose of docking by using the groove of the shaft with the tab inside the circular ring. When the joint is inserted and pulled out, the ferrule expands and deforms, and generally, the material used as the ferrule is the more elastic material.
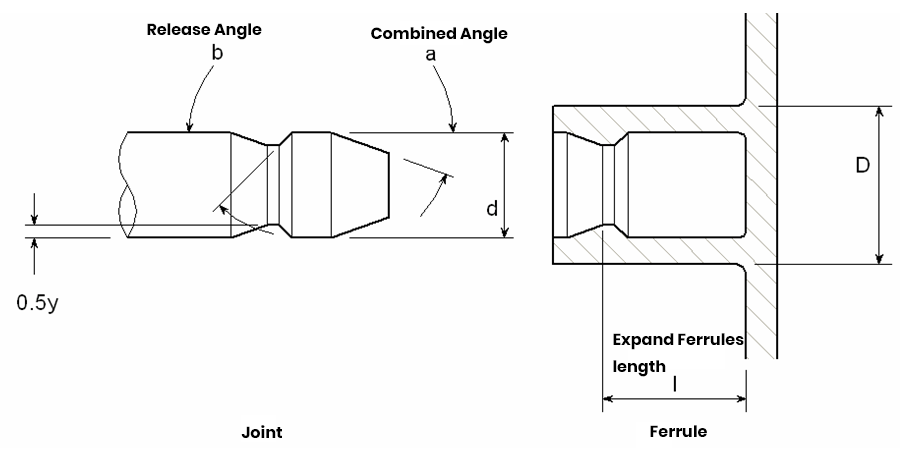
The maximum size of the tab of a circular snap can be calculated using the following formula:
- y=Sd((K+v ferrules)/E ferrules + (1 – v axis)/E axis)/K
Where S is the design stress, v is the Poisson’s ratio, E is the modulus of elasticity, K is the geometric coefficient, and the following formula can calculate K:
- K = (1 + (d/D)2)/(1 – (d/D)2)
The following equation can calculate the expansion force acting on the ferrule:
- P = (tan a+μ)/Sydlπ/K
where μ is the coefficient of friction.
The Poisson’s ratios for some materials without filler are given in Table 4 below, and the friction coefficients are shown in Table 3.
Plastic Material | Poisson’s ratios(μ) |
PS | 0.38 |
PMMA | 0.4 |
LDPE | 0.49 |
HDPE | 0.47 |
PP | 0.43 |
PA | 0.45 |
PC | 0.42 |
PVC | 0.42 |
PPO | 0.41 |
PPS | 0.42 |
Steel | 0.28 |
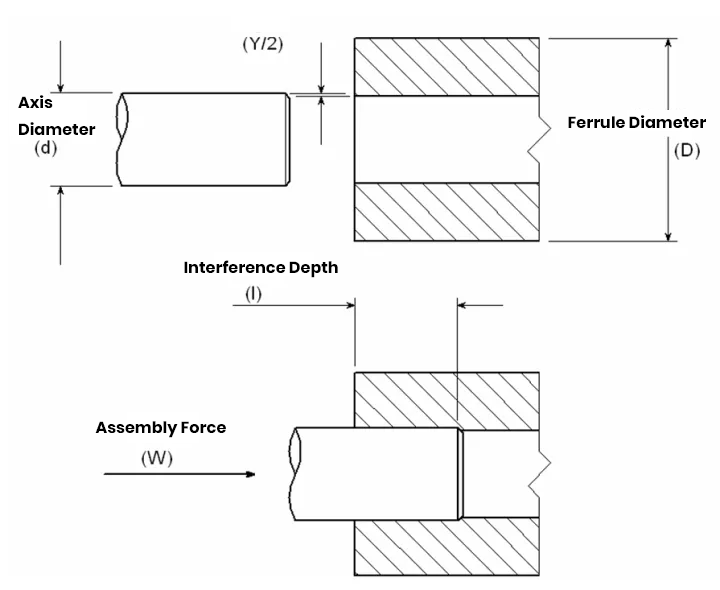
Interference Connection
Bore and shaft are connected by interference fit to transfer torque and other functions; interference connection is relatively convenient and simple. The main consideration in the design process is the amount of interference. If the amount of interference is too small, the connection is not reliable, and if the interference is too large, it is difficult to assemble and also easy to break.
In the design process, the tolerance of the hole and the shaft and the working temperature should be considered because the temperature will directly affect the size of the interference. In most cases, the shaft is generally a metal shaft, and to ensure the reliability of the connection, knurled grooves are generally added to the mating shaft during design. The general amount of interference can be calculated by the following formula:
- Y=Sd( (K+v sleeve)/E sleeve)/K
Where S is the design stress, v is Poisson’s ratio, E is the modulus of elasticity, K is the geometric coefficient, and the following formula can calculate K:
- K = (1+(d/D)2)/(1 – (d/D)2)
The following formula can calculate the mating force:
- W = Sdlπμ/K
μ is the friction coefficient, and l is the mating length. The friction coefficient and Poisson’s ratio are shown in Table 3 and Table 4
In addition, there are other methods of joining plastic parts, such as hot riveting, welding, and ultrasonic welding.
Effect of Tolerance
Most plastic products can achieve high precision fit dimensional tolerances, while some shrinkage and soft materials are more difficult to control. Therefore, in the product design process, it is necessary to consider the product’s use environment, plastic material, product shape, etc., to set the tightness of tolerance. Because the customer’s requirements are getting higher and higher, the previous concept of fit has to be improved slowly. Fit, precision, and appearance are to be brought out in the product simultaneously.
A high degree of precision in tolerances results in a relatively higher quality product, but with it comes increased costs and more time to meet the requirements. Injection molding is generally classified into three quality levels: general-purpose injection molding, medium precision molding, and precision injection molding.
General-purpose injection molding requires a low level of quality control and is characterized by low return rates and fast production cycles. Medium-precision injection molding can be more expensive because it requires higher demands on the mold and production process, requiring frequent quality checks. The third type, precision injection molding, requires precise molds, optimal production conditions, and 100% continuous production monitoring. This affects the production cycle time and increases the unit and quality control costs. From the point of view of product quality, of course, the higher the accuracy, the better, but from the point of view of economic production costs, the lower, the cheaper. As a designer at this time must choose between the two.
Generally speaking, to meet the performance, and appearance requirements, fit requirements under the premise of appropriate relaxation of the tolerance of non-critical dimensions.
Choosing the right material
In general, there is no such thing as a bad material, only the wrong material used in a particular area. Therefore, it is essential for the designer to understand the properties of the various materials available thoroughly, carefully test these materials, and study their influence on the performance of molded and processed products in relation to various factors.
The most commonly used in injection molding is thermoplastic. It can be further divided into amorphous plastics and semi-crystalline plastics. These two materials differ significantly in their molecular structure and properties affected by crystallization. In general, semi-crystalline thermoplastics are mainly used for mechanically robust parts, while amorphous thermoplastics are often used for housings because they are not easily bent.
Thermoplastics are available in unreinforced, glass fiber reinforced, mineral, and vitreous-filled varieties. Glass fibers are primarily used to increase strength, stiffness, and application temperature; minerals have a lower reinforcement effect and are primarily used to reduce warpage. The exact amount of change in plastic properties with the addition of reinforcements should be verified by consultation with the material supplier or experimentally.
Some thermoplastic materials, particularly PA6 and PA66, are highly hygroscopic. This can have a significant impact on their mechanical properties and dimensional stability.
Some requirements are related to processing considerations and assembly. It is also essential to investigate the concentration of several different functions in one part, which can save expensive assembly costs. This guideline is handy for calculating production costs. In the price calculation, it can be seen that not only the price of raw materials should be taken into account, but it should also be noted that materials with high performance (rigidity, toughness) can lead to thinner wall thicknesses and, thus, shorter production cycles. Therefore, it is essential to list and evaluate all the criteria systematically.
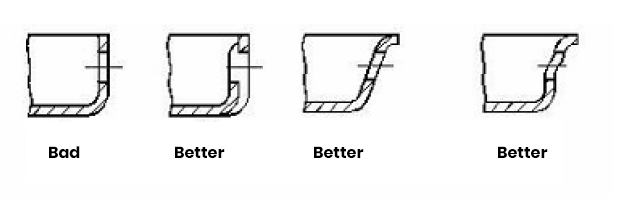
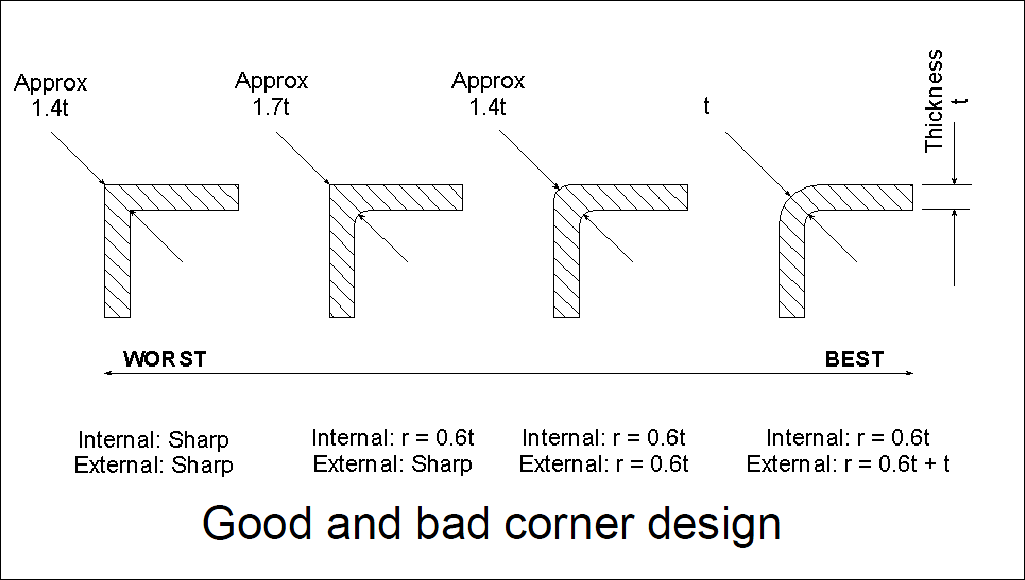
Rounded corners
Sharp corners often lead to defects and stress concentrations in the part, where the concentrated stresses can break under load or impact. Larger rounded corners solve this drawback, reducing the stress concentration factor and allowing the flow of plastic to be smoother and the finished part to be unmolded more easily. If the inner corners are rounded and the outer corners are sharp, the corners will still be thicker than the rest, and shrinkage will still occur; we can make the wall thickness uniform by rounding both the inner and outer corners, in which case the outer corners are the sum of the inner corners plus the base wall thickness.
The design guideline of the corner bit also applies to the overhanging beam-type fastening. As this fastening method is required to bend the suspension beam arm embedded, the design of the corner position illustrates that if the corner arc position R is too small will cause its stress concentration coefficient to be too large; therefore, the product is easy to break when bending, arc position R is too large, it is easy to appear shrinkage lines and hollow. Therefore, the arc position and wall thickness are a specific ratio. Generally, between 0.2 to 0.6, the ideal value is 0.5 or so.
Conclusion
Injection mold structure design is a complex process that requires consideration of several vital elements. Wall thickness, draft angle, stiffening bar, pillar, snap, and tolerance are all critical components that must be considered when designing an injection mold. Each element plays a vital role in the overall performance of the mold and must be carefully considered to ensure the best possible outcome. With the right design, injection molds can create high-quality parts with minimal waste and cost.
I hope everyone can become a successful structural design engineer.
